报告人：雷金龙（同济大学电子与信息工程学院）

报告时间：2020年6月11日14:00-15:00

报告地点：南楼208教室

腾讯会议：516 948 450

报告摘要: This talk considers distributed stochastic optimization over i.i.d. random networks, where agents collaboratively minimize the average of all agents' local expectation-valued cost functions. Due to the stochasticity in gradient observations, distributedness of local functions, and randomness of communication topologies, distributed algorithms with a convergence guarantee under fixed step-sizes have not been achieved yet. This work incorporates a variable sample-size scheme into the distributed stochastic gradient tracking algorithm, such that the local gradients are estimated by an increasing batch-size of sampled gradients. We show that all agents’ iterates converge almost surely to the same optimal solution under fixed step-sizes for convex problems. When local cost functions are strongly convex, we further prove that the iterates converge in a mean-squared sense to the unique optimal solution at a geometric rate, and establish the iteration and oracle complexity for obtaining an  -optimal solution. Specifically, the iteration number 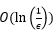 matches that established in deterministic regimes, and the total number of sampled gradients  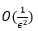 is of the same order as that of centralized SGD methods.

个人简介： 雷金龙，同济大学电子与信息工程学院“青年百人B计划”特聘研究员。2011年于中国科学技术大学获得学士学位，2016年于中国科学院数学与系统科学研究院获得理学博士学位。 2016年8月- 2019年9月，在美国宾夕法尼亚州立大学工业工程系从事博士后研究。 在运筹学与控制领域 Operations Research,  IEEE Transcations on Automatic Control,  SIAM Journal on Optimization, Mathematics of Operations Reseach等期刊上发表多篇论文，并获得2019-2021年度中国自动化学会青年人才托举工程项目。主要研究方向是不确定信息下多智能体网络优化与非合作博弈的分析与设计理论，包括随机纳什博弈、随机非凸优化、随机逼近、分布式估计与分布式优化等。